The alpha decay of radon 198, a captivating phenomenon in nuclear physics, invites us to delve into its intricacies. This process, characterized by the emission of alpha particles, offers insights into the behavior of radioactive isotopes and their impact on various scientific disciplines.
Radon 198, a naturally occurring isotope of radon, undergoes alpha decay to transform into a more stable nuclide. This decay process releases a substantial amount of energy, making it a subject of significant interest in fields such as medicine, geology, and environmental science.
Introduction: The Alpha Decay Of Radon 198

Alpha decay is a type of radioactive decay in which an atomic nucleus emits an alpha particle, which is a helium nucleus consisting of two protons and two neutrons. This process results in the transformation of the parent nucleus into a new nucleus with an atomic number decreased by 2 and a mass number decreased by 4.
Radon-198 is a radioactive isotope of radon with an atomic number of 86 and a mass number of 198. It has a half-life of approximately 1.89 days and undergoes alpha decay to form polonium-214.
Properties of Radon-198, The alpha decay of radon 198
- Radon-198 is a noble gas, meaning it is colorless, odorless, and tasteless.
- It is a naturally occurring radioactive isotope found in small amounts in the Earth’s atmosphere.
- Radon-198 is a decay product of uranium-238 and is often used as a tracer for uranium exploration.
- Exposure to high levels of radon-198 can increase the risk of lung cancer.
Alpha Decay Process
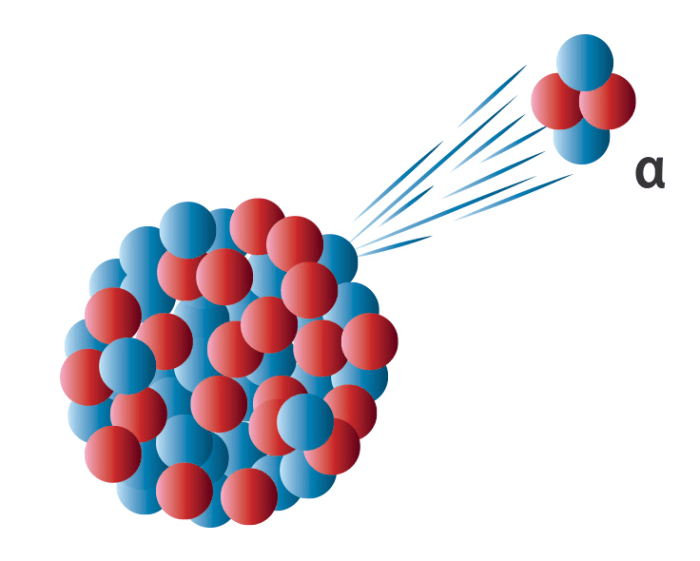
Alpha decay is a type of radioactive decay in which an unstable atomic nucleus emits an alpha particle, resulting in the formation of a new nucleus with a lower atomic number and mass number. In the case of radon-198, the alpha decay process can be represented by the following nuclear equation:
198Rn → 194Po + 4He
During this decay process, the radon-198 nucleus emits an alpha particle, which consists of two protons and two neutrons, effectively reducing the atomic number by two and the mass number by four. The resulting nucleus is polonium-194.
Energy Released
The alpha decay process releases a significant amount of energy, which is carried away by the alpha particle. This energy is due to the difference in mass between the parent nucleus (radon-198) and the daughter nucleus (polonium-194) plus the alpha particle.
The alpha decay of radon 198, a radioactive isotope of radon, results in the emission of an alpha particle. This process transforms radon 198 into polonium 214. Incidentally, John Gray bought a basic car recently. Continuing with the alpha decay of radon 198, the emitted alpha particle has an energy of 5.49 MeV and a range of about 4 cm in air.
The mass defect, which is the difference in mass, is converted into energy according to Einstein’s famous equation, E=mc². This released energy appears as kinetic energy of the alpha particle.
Daughter Nuclide

The alpha decay of radon-198 results in the formation of a daughter nuclide, which is a new atomic nucleus created from the decay process.
The daughter nuclide produced in the alpha decay of radon-198 is polonium-214.
Properties and Characteristics of Polonium-214
Polonium-214 is a radioactive element with the atomic number 84 and atomic mass 214. It is a member of the polonium group of elements and is a heavy metal.
Polonium-214 has a half-life of 164.3 microseconds, which means that it decays rapidly by emitting an alpha particle and transforming into lead-210.
Half-Life and Decay Constant
In radioactive decay, the half-life of a substance is the amount of time it takes for half of its atoms to decay. It is a fundamental property of each radioactive isotope and is an important factor in understanding and predicting the behavior of radioactive materials.
The decay constant, denoted by λ, is a mathematical constant that describes the rate of radioactive decay. It is related to the half-life by the following equation:
t1/2= ln(2) / λ
Where:
- t 1/2is the half-life
- λ is the decay constant
Calculating Half-Life of Radon-198
The decay constant of radon-198 is 2.097 × 10 -6s -1. Using the equation above, we can calculate the half-life of radon-198 as follows:
t1/2= ln(2) / λ= ln(2) / (2.097 × 10 -6s -1)≈ 3.3 days
Therefore, the half-life of radon-198 is approximately 3.3 days.
Applications and Significance
Radon-198 finds diverse applications in various fields, including medicine and geology. Its unique properties have led to its utilization in specific procedures and investigations.
In medicine, radon-198 is employed in a specialized technique known as radon therapy. This therapy involves the controlled exposure of patients to low doses of radon gas to alleviate pain and inflammation associated with certain conditions, such as arthritis and chronic pain syndromes.
Environmental and Health Implications
The decay of radon-198 poses potential environmental and health concerns. Radon gas, being radioactive, can accumulate in enclosed spaces, particularly in homes and buildings. Prolonged exposure to high levels of radon can increase the risk of developing lung cancer.
To mitigate these risks, proper ventilation and radon testing in homes and workplaces are crucial. Radon mitigation systems can be installed to reduce radon levels and ensure a safe and healthy indoor environment.
Frequently Asked Questions
What is alpha decay?
Alpha decay is a type of radioactive decay in which an atomic nucleus emits an alpha particle, consisting of two protons and two neutrons, resulting in the transformation of the parent nuclide into a new nuclide with a lower atomic number and mass number.
What is the significance of the half-life in alpha decay?
The half-life of a radioactive isotope is the time it takes for half of the atoms in a sample to decay. It provides valuable information about the stability of the isotope and helps predict its behavior in various applications.
What are the applications of radon 198?
Radon 198 finds applications in various fields, including medicine (brachytherapy), geology (uranium exploration), and environmental science (studying radon gas concentrations in soil and air).